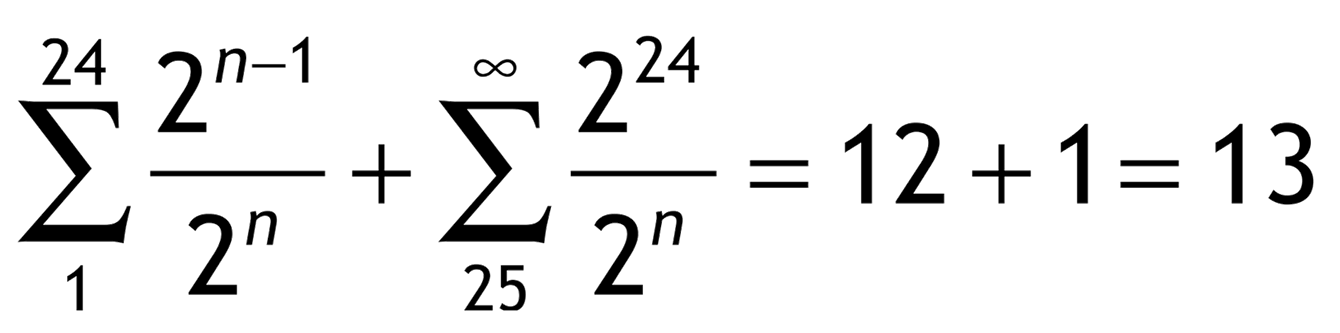Origins of probability calculus

Since the ancient times, man has been interested in games of chance; it is known that the use of jacks is as old as humanity itself and seems to be the predecessor of the dice and roulette. The first known dice was made of clay covered with leather, it was found north of Irak and dates from the beginning of the third millennium b.C.

The Greek, who had an Egyptian goddess of luck named Tique , made polyhedral dice that resembled the platonic solids, some are kept at the Louvre museum in Paris.

According to the Bible, around the year 1000 b.C., the Israelis elected a king by a draw (Samuel 10:20-24).

The probability calculus very slowly became part of the mathematics field. The first known document where games of chance were analyzed in a systematic way is the Liber de ludo aleae (Games of Chance Guide), written by Gerolamo Cardano around 1550, but published a hundred years after his death. The great Galileo also took an interest in games of chance and wrote a brochure called Soprale scopere dei dadi (Findings on dice games) published in 1718.

Below we will see some concrete and practical problems from which the mathematic model, that today is called probability calculus, was formed.

The duke of Tuscany's problem (1560)

The duke of Tuscany was an inveterate player. He had observed that in a game in which three dice are tossed and the points added, number 10 appeared more often than number 9. However, according to de duke, both numbers can be obtained in the six following ways.

1+2+6=9 \ 1+3+6=10
1+3+5=9 \ 1+4+5=10
1+4+4=9 \ 2+2+6=10
2+2+5=9 \ 2+3+5=10
2+3+4=9 \ 2+4+4=10
3+3+3=9 \ 3+3+4=10

Cardano was consulted and studied the problem but he didn't find a conclusive answer. It was Galileo who 50 years later found the solution; to do so he counted all the possible cases and for the first time he presented the data in distribution tables, like the following regarding to the previous problem:

Number 9 is obtained in the following ways: (6,1,2), (6,2,1), (5,1,3), (5,2,2), (5,3,1), (4,1,4), . . . , (1,6,2). There are 25 ways to obtain 9. Number 10 can be obtained in 27 different ways: (6,1,3), (6,2,2), (6,3,1), (5,1,4), (5,2,3),(5,3,2), . . .

Therefore, it is normal for number 10 to appear more often than number 9.

Total of points obtained with three dice 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Number of ways to
obtain		 1 3 6 10 15 21 25 27 27 25 21 15 10 6 3 1

Chevalier de Méré's problems (1650)

Antoine de Gambaud, Chevalier de Méré, was a player, man of literature and a very well known courtier in the court of king Louis XIV of France. His first problem resembles the one of the duke of Tuscany: ¿How can number 11 occur more often than number 12 when three dice are rolled, if both numbers can be formed in 6 different ways? The Chevallier de Méré consulted his friend Blaise Pascal, who by means of this question, became interested in probability and solved this problem (using the same method as Galileo) and many more.

To solve the second problem of the Chevallier de Méré, Pascal asked Fermat for his opinion and wrote (1654): "The Chevallier de Méré is very talented, but he is not a mathematician and that, as you know, is a great defect." This is the problem:

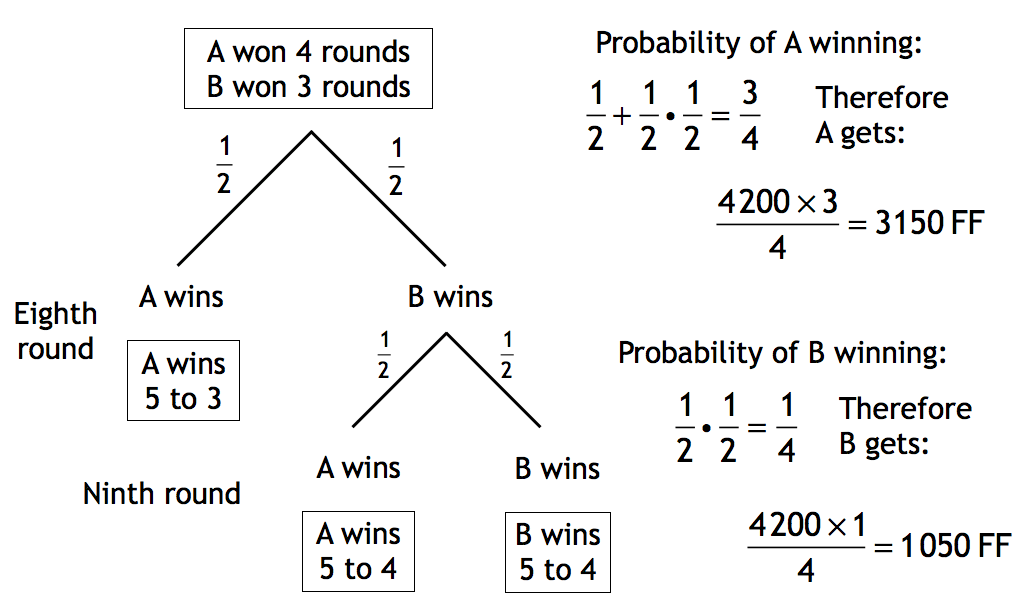
Two persons, A and B, play a game where both have the same probability of winning (that is 1/2; like for example, tossing a coin). The first to win 5 times gets the prize of 4,200 French Francs. Unfortunately after tossing the coin seven times the match ends; by that moment A has won 4 times and B has won 3 times.

¿How should the prize be divided between the two players? Several solutions were proposed:

a) Divide the prize in proportions of 4 and 3, given that the match ended that way; so, A would get 2,400 FF and B would get 1,800 FF.

b) Divide the prize in proportions (5-3) and (5-4), that is 2 and 1.
In that case, A would get 2,800 FF and B 1,400 FF.

Neither solution convinced the players, until Pascal and Fermat proposed a scheme that took into account the fact that A had already won 4 throws. The analysis made here started the study of "conditional probability", and the method used is applied today in many cases ranging from business to medicine. A tree diagram helps the visual representation of the problem:


The problem of d'Alembert (18th Century)

Jean Le Rond d'Alembert was a famous French mathematician from the 18th Century; he is also famous for making a mistake in the following problem he was presented with in 1754:

¿What is the probability of obtaining heads at least one time when tossing two coins?

D'Alembert analyzed the problem taking three possibilities into account:

Heads in the first event
Heads in the second event
No heads.

As there are 3 possible cases and two unfavorable, the probability is 2/3.

The correct analysis is to note that there are 4 possible cases: heads-heads, heads-tails, tails-heads, tails-tails; in 3 of these cases heads occurs at least one time, the probability in question is then 3/4.

The paradox of Saint Petersburg (18th century)

In 1725, Daniel and Nicholas Bernoulli taught mathematics in the academy of the city of Saint Petersburg (that had recently been created by Peter the Great of Russia), Nicholas had proposed the following problem in the Commentarii of the academy, this problem is known as de paradox of Saint Petersburg.

The game consists in tossing a coin until heads appears. If heads occurs in the first throw, Daniel must pay one krone to Nicholas. If tails occurs first and heads second (T, H), Daniel must pay 2 krones.

If heads occurs first in the third throw (T, T, H) Daniel must pay 4 krones.
If the series of throws gives T, T, T, H, Daniel must pay 8 krones
etc. . . .
If the series gives T, T, T, . . . , T, H, with n throws, Daniel must pay 2(n-1) krones.

In other words,
the probability of Nicholas getting 1 krone is 1/2
the probability of Nicholas getting 2 krones is 1/4
the probability of Nicholas getting 4 krones is 1/8
etc. . . .

The problem is: ¿How much does Nicholas have to pay to Daniel if he wants the game to be fair?
What Nicholas can win (the expected value) is:

5
an infinite addition; hence, in theory, he would have to pay an infinite amount of money for the game to be fair. However, common sense suggests that it is only a small quantity of money what has to be paid.

Georges Louis Leclerc, count de Buffon, a well known french naturalist (1707-1788), made an empirical test: he hired a boy to toss a coin many times (in those days there were no computers to simulate experiments). The boy made 2,084 throws, and discovered that Nicholas would have to pay Daniel 10,057 krones, an average of 5 krones per event, not an infinite amount (during the first simulated experiment for 1,061 throws 1 krone was paid; for 494 throws 2 krones were paid, etc. ...)

Count de Buffon was the first to emphasize the importance of verifying a theory with real experiments.

The paradox of Saint Petersburg has been explained in several ways. Daniel Bernoulli invented the principle of "moral expectation", and described a new function which he called "utility function": the value of a small quantity of money is not the same to a rich person than to a poor person (he defined the "moral expectation" as the mathematical expectation of the logarithm of the fortune).

Another explanation is that given the finite character of Nicholas' fortune, it is impossible for him to pay Daniel if heads takes too long to appear. In other words "the infinite mathematical expectation" is explained by the slim possibility of winning an enormous (infinite) amount if a long series of heads occurs. 

To sum up, the paradox of Saint Petersburg is a particular case of the general problem of doubling the bet in gambling; a system in which in theory it is impossible to be defeated (because heads will eventually appear); but in fact it is a sure way to lose, since the amount of money available to the player is in most cases limited and smaller than the bank's. To ensure even more their probability of not losing, the casinos fix a maximum amount for all bets.

The well known Swiss mathematician Gabriel Cramer  (1704-1752) explains that the fortune of the bank, although it can be great, it's always limited. Say that the bank's capital is $ 224, the player has a 1/(2n) chance of getting $ 2n-1 when n is less than 25, but after all he could only receive $ 224. Hence his mathematical expectancy is $ 13, which is very reasonable. These are Cramer's calculations:

6

Direct quote from: PERERO, Mariano. Historias e historia de las matemáticas. Editorial iberoamérica, México. 1994, pp. 86-88. Tr. Probabilidad y Estadística, F.I. UNAM

Go back